Example: Power Dissipation in Mixed Circuit with \( R_1 = 150 \, \Omega \), \( R_2 = 180 \, \Omega \), and \( R_3 = 220 \, \Omega \)

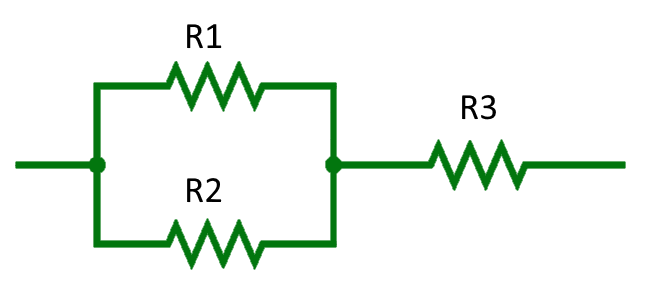
Let's calculate the total resistance, the current through the circuit, and the power dissipated by each resistor when \( R_1 = 150 \, \Omega \), \( R_2 = 180 \, \Omega \), and \( R_3 = 220 \, \Omega \), with a total voltage \( V_{total} \).

1. Total Resistance Calculation: For two resistors, \( R_1 = 150 \, \Omega \) and \( R_2 = 180 \, \Omega \), in parallel, the equivalent resistance \( R_{12} \) is given by:
   \[ \frac{1}{R_{12}} = \frac{1}{R_1} + \frac{1}{R_2} \]
   \[ \frac{1}{R_{12}} = \frac{1}{150} + \frac{1}{180} \]
   \[ \frac{1}{R_{12}} = \frac{180 + 150}{150 \times 180} \]
   \[ R_{12} = \frac{150 \times 180}{330} \approx 81.82 \, \Omega \]
2. Total Resistance of the Mixed Circuit: The total resistance \( R_{total} \) is the sum of \( R_{12} \) and \( R_3 \):
   \[ R_{total} = R_{12} + R_3 \]
   \[ R_{total} = 81.82 \, \Omega + 220 \, \Omega \approx 301.82 \, \Omega \]
3. Current Through the Circuit: The current \( I \) through the series circuit is the same for all components and is calculated using Ohm's law:
   \[ I = \frac{V_{total}}{R_{total}} \]
4. Voltage Drop Across Each Resistor: The voltage drop \( V_{12} \) across the parallel combination and \( V_3 \) across \( R_3 \) can be calculated as:
   \[ V_{12} = I \times R_{12} \quad \text{and} \quad V_3 = I \times R_3 \]
5. Power Dissipated by Each Resistor: The power dissipated by each resistor can be calculated as follows:
   \[ P_1 = \left( \frac{V_{12}}{R_1} \right)^2 \times R_1 \quad \text{and} \quad P_2 = \left( \frac{V_{12}}{R_2} \right)^2 \times R_2 \]
   \[ P_3 = I^2 \times R_3 \]
6. Example Calculation: Assume the total voltage \( V_{total} = 10 \, \text{V} \).
   \[ I = \frac{10 \, \text{V}}{301.82 \, \Omega} \approx 0.0331 \, \text{A} \]
   \[ V_{12} = 0.0331 \, \text{A} \times 81.82 \, \Omega \approx 2.71 \, \text{V} \]
   \[ V_3 = 0.0331 \, \text{A} \times 220 \, \Omega \approx 7.28 \, \text{V} \]
   \[ P_1 = \left( \frac{2.71 \, \text{V}}{150 \, \Omega} \right)^2 \times 150 \, \Omega \approx 0.049 \, \text{W} \]
   \[ P_2 = \left( \frac{2.71 \, \text{V}}{180 \, \Omega} \right)^2 \times 180 \, \Omega \approx 0.041 \, \text{W} \]
   \[ P_3 = (0.0331 \, \text{A})^2 \times 220 \, \Omega \approx 0.241 \, \text{W} \]