How Can One Make a 6.8 µF Capacitor Using a Combination of Other Capacitors?
See below how to make a 6.8 µF equivalent capacitor by using other different capacitors.
Capacitor Replacement Calculator
Type a value in box below. Then press "Calculate"
Answer
Below you can find a series of capacitor combinations to replace a 6.8 µF capacitor.
Series Combinations:
For two capacitors in series, the total capacitance is calculated as:
\(C_{total} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2}}\)
For example, with 8.2 µF + 40 µF in series = 6.8 µF (exact)
\(C_{total} = \frac{1}{\frac{1}{8.2} + \frac{1}{40}} \approx 6.8 \mu F\)
- 8.2 µF + 40 µF in series = 6.8 µF (exact)
- 8.2 µF + 39 µF in series = 6.78 µF (error: 0.29%)
- 10 µF + 21 µF in series = 6.77 µF (error: 0.44%)
- 12 µF + 16 µF in series = 6.86 µF (error: 0.88%)
- 10 µF + 22 µF in series = 6.88 µF (error: 1.18%)
- 8.2 µF + 36 µF in series = 6.68 µF (error: 1.76%)
- 8 µF + 40 µF in series = 6.67 µF (error: 1.91%)
- 10 µF + 20 µF in series = 6.67 µF (error: 1.91%)
- 12 µF + 15 µF in series = 6.67 µF (error: 1.91%)
- 8 µF + 39 µF in series = 6.64 µF (error: 2.35%)
- 8.2 µF + 35 µF in series = 6.64 µF (error: 2.35%)
- 8.2 µF + 33 µF in series = 6.57 µF (error: 3.38%)
- 8 µF + 36 µF in series = 6.55 µF (error: 3.68%)
- 10 µF + 24 µF in series = 7.06 µF (error: 3.82%)
- 8 µF + 35 µF in series = 6.51 µF (error: 4.26%)
- 10 µF + 25 µF in series = 7.14 µF (error: 5%)
- 8 µF + 33 µF in series = 6.44 µF (error: 5.29%)
- 8.2 µF + 30 µF in series = 6.44 µF (error: 5.29%)
- 10 µF + 18 µF in series = 6.43 µF (error: 5.44%)
- 12 µF + 18 µF in series = 7.2 µF (error: 5.88%)
- 8 µF + 30 µF in series = 6.32 µF (error: 7.06%)
- 10 µF + 27 µF in series = 7.3 µF (error: 7.35%)
- 8.2 µF + 27 µF in series = 6.29 µF (error: 7.5%)
- 8 µF + 27 µF in series = 6.17 µF (error: 9.26%)
- 8.2 µF + 25 µF in series = 6.17 µF (error: 9.26%)
- 10 µF + 16 µF in series = 6.15 µF (error: 9.56%)
- 8.2 µF + 24 µF in series = 6.11 µF (error: 10.15%)
- 10 µF + 30 µF in series = 7.5 µF (error: 10.29%)
- 12 µF + 20 µF in series = 7.5 µF (error: 10.29%)
- 15 µF + 15 µF in series = 7.5 µF (error: 10.29%)
- 8 µF + 25 µF in series = 6.06 µF (error: 10.88%)
- 8 µF + 24 µF in series = 6 µF (error: 11.76%)
- 10 µF + 15 µF in series = 6 µF (error: 11.76%)
- 12 µF + 12 µF in series = 6 µF (error: 11.76%)
- 8.2 µF + 22 µF in series = 5.97 µF (error: 12.21%)
- 12 µF + 21 µF in series = 7.64 µF (error: 12.35%)
- 10 µF + 33 µF in series = 7.67 µF (error: 12.79%)
- 8.2 µF + 21 µF in series = 5.9 µF (error: 13.24%)
- 8 µF + 22 µF in series = 5.87 µF (error: 13.68%)
- 15 µF + 16 µF in series = 7.74 µF (error: 13.82%)
- 12 µF + 22 µF in series = 7.76 µF (error: 14.12%)
- 7 µF + 35 µF in series = 5.83 µF (error: 14.26%)
- 8.2 µF + 20 µF in series = 5.82 µF (error: 14.41%)
- 10 µF + 35 µF in series = 7.78 µF (error: 14.41%)
- 8 µF + 21 µF in series = 5.79 µF (error: 14.85%)
- 7 µF + 33 µF in series = 5.78 µF (error: 15%)
Parallel Combinations:
For two capacitors in parallel, you add the capacitances directly:
\(C_{total} = C_1 + C_2\)
For example, with 2 µF + 4.7 µF in parallel = 6.7 µF (error: 1.47%)
\(C_{total} = 2 \mu F + 4.7 \mu F = 6.7 \mu F\)
- 2 µF + 4.7 µF in parallel = 6.7 µF (error: 1.47%)
- 2.2 µF + 4.7 µF in parallel = 6.9 µF (error: 1.47%)
- 2 µF + 5 µF in parallel = 7 µF (error: 2.94%)
- 3 µF + 4 µF in parallel = 7 µF (error: 2.94%)
- 3.3 µF + 3.3 µF in parallel = 6.6 µF (error: 2.94%)
- 1.5 µF + 5 µF in parallel = 6.5 µF (error: 4.41%)
- 1.5 µF + 5.6 µF in parallel = 7.1 µF (error: 4.41%)
- 2.2 µF + 5 µF in parallel = 7.2 µF (error: 5.88%)
- 3 µF + 3.3 µF in parallel = 6.3 µF (error: 7.35%)
- 3.3 µF + 4 µF in parallel = 7.3 µF (error: 7.35%)
- 1.5 µF + 4.7 µF in parallel = 6.2 µF (error: 8.82%)
- 2.2 µF + 4 µF in parallel = 6.2 µF (error: 8.82%)
- 1 µF + 5 µF in parallel = 6 µF (error: 11.76%)
- 2 µF + 4 µF in parallel = 6 µF (error: 11.76%)
- 2 µF + 5.6 µF in parallel = 7.6 µF (error: 11.76%)
- 3 µF + 3 µF in parallel = 6 µF (error: 11.76%)
- 3 µF + 4.7 µF in parallel = 7.7 µF (error: 13.24%)
- 2.2 µF + 5.6 µF in parallel = 7.8 µF (error: 14.71%)
Mixed Combinations:
For a mixed combination, first calculate the series capacitance:
\(C_{series} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2}}\)
Then, place this combination in parallel with the third capacitor:
\(C_{total} = C_{series} + C_3\)
For example, with 2 µF + 3 µF in series with 5.6 µF in parallel = 6.8 µF (exact)
\(C_{series} = \frac{1}{\frac{1}{2} + \frac{1}{3}} \approx 1.2 \mu F\)
\(C_{total} = 1.2 \mu F + 5.6 \mu F \approx 6.8 \mu F\)
- 2 µF + 3 µF in series with 5.6 µF in parallel = 6.8 µF (exact)
- 3 µF + 2 µF in series with 5.6 µF in parallel = 6.8 µF (exact)
- 3 µF + 7 µF in series with 4.7 µF in parallel = 6.8 µF (exact)
- 4.7 µF + 5.6 µF in parallel with 20 µF in series = 6.8 µF (exact)
- 5.6 µF + 4.7 µF in parallel with 20 µF in series = 6.8 µF (exact)
- 5.6 µF + 5.6 µF in series with 4 µF in parallel = 6.8 µF (exact)
- 7 µF + 3 µF in series with 4.7 µF in parallel = 6.8 µF (exact)
- 7 µF + 7 µF in series with 3.3 µF in parallel = 6.8 µF (exact)
- 10 µF + 30 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 15 µF + 25 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 16 µF + 24 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 18 µF + 22 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 20 µF + 20 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 22 µF + 18 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 24 µF + 16 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 25 µF + 15 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 30 µF + 10 µF in parallel with 8.2 µF in series = 6.8 µF (exact)
- 3.3 µF + 4 µF in series with 5 µF in parallel = 6.81 µF (error: 0.15%)
- 4 µF + 3.3 µF in series with 5 µF in parallel = 6.81 µF (error: 0.15%)
- 4.7 µF + 7 µF in series with 4 µF in parallel = 6.81 µF (error: 0.15%)
- 5 µF + 6.8 µF in parallel with 16 µF in series = 6.79 µF (error: 0.15%)
- 5.6 µF + 6.8 µF in parallel with 15 µF in series = 6.79 µF (error: 0.15%)
- 6.8 µF + 5 µF in parallel with 16 µF in series = 6.79 µF (error: 0.15%)
- 6.8 µF + 5.6 µF in parallel with 15 µF in series = 6.79 µF (error: 0.15%)
- 7 µF + 4.7 µF in series with 4 µF in parallel = 6.81 µF (error: 0.15%)
- 1.5 µF + 5.6 µF in series with 5.6 µF in parallel = 6.78 µF (error: 0.29%)
- 3 µF + 6.8 µF in series with 4.7 µF in parallel = 6.78 µF (error: 0.29%)
- 3.3 µF + 5.6 µF in series with 4.7 µF in parallel = 6.78 µF (error: 0.29%)
- 4.7 µF + 6.8 µF in series with 4 µF in parallel = 6.78 µF (error: 0.29%)
- 5.6 µF + 1.5 µF in series with 5.6 µF in parallel = 6.78 µF (error: 0.29%)
- 5.6 µF + 3.3 µF in series with 4.7 µF in parallel = 6.78 µF (error: 0.29%)
- 5.6 µF + 10 µF in parallel with 12 µF in series = 6.78 µF (error: 0.29%)
- 6.8 µF + 3 µF in series with 4.7 µF in parallel = 6.78 µF (error: 0.29%)
- 6.8 µF + 4.7 µF in series with 4 µF in parallel = 6.78 µF (error: 0.29%)
- 7 µF + 8.2 µF in series with 3 µF in parallel = 6.78 µF (error: 0.29%)
- 8.2 µF + 7 µF in series with 3 µF in parallel = 6.78 µF (error: 0.29%)
- 10 µF + 5.6 µF in parallel with 12 µF in series = 6.78 µF (error: 0.29%)
- 12 µF + 27 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 15 µF + 24 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 18 µF + 21 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 21 µF + 18 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 24 µF + 15 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 27 µF + 12 µF in parallel with 8.2 µF in series = 6.78 µF (error: 0.29%)
- 5.6 µF + 12 µF in series with 3 µF in parallel = 6.82 µF (error: 0.29%)
- 12 µF + 5.6 µF in series with 3 µF in parallel = 6.82 µF (error: 0.29%)
- 3 µF + 4.7 µF in series with 5 µF in parallel = 6.83 µF (error: 0.44%)
- 4 µF + 7 µF in parallel with 18 µF in series = 6.83 µF (error: 0.44%)
- 4.7 µF + 3 µF in series with 5 µF in parallel = 6.83 µF (error: 0.44%)
- 5 µF + 5 µF in parallel with 21 µF in series = 6.77 µF (error: 0.44%)
- 5 µF + 12 µF in series with 3.3 µF in parallel = 6.83 µF (error: 0.44%)
How to Use This Calculator
To use this Capacitor Combination or Replacement Calculator, fill in the desired total capacitance value in the provided field and click on the 'Calculate' button. The calculator will find numerous combinations and select the best ones. You will receive various combinations made up of capacitors with their respective percentage error or exact values to help you choose the best option for your needs.
Capacitor Values Table
Our Capacitor Combination Calculator works combining the values of capacitances in parallel, series or mixed. It uses the following standard capacitance values to find the best equivalent capacitor configurations. Each value is measured in microfarads (µF).
| Common Capacitor Values | |||
|---|---|---|---|
| 0.1 µF | 0.15 µF | 0.22 µF | 0.33 µF |
| 0.47 µF | 0.68 µF | 1 µF | 1.5 µF |
| 2 µF | 2.2 µF | 3 µF | 3.3 µF |
| 4 µF | 4.7 µF | 5 µF | 5.6 µF |
| 6.8 µF | 7 µF | 8 µF | 8.2 µF |
| 10 µF | 12 µF | 15 µF | 16 µF |
| 18 µF | 20 µF | 21 µF | 22 µF |
| 24 µF | 25 µF | 27 µF | 30 µF |
| 33 µF | 35 µF | 36 µF | 39 µF |
| 40 µF | 43 µF | 47 µF | 50 µF |
| 53 µF | 56 µF | 60 µF | 68 µF |
| 72 µF | 75 µF | 82 µF | 88 µF |
| 100 µF | 108 µF | 120 µF | 124 µF |
| 130 µF | 140 µF | 145 µF | 150 µF |
| 161 µF | 170 µF | 180 µF | 189 µF |
| Common Capacitor Values | |||
|---|---|---|---|
| 200 µF | 210 µF | 216 µF | 220 µF |
| 230 µF | 233 µF | 240 µF | 243 µF |
| 250 µF | 270 µF | 300 µF | 320 µF |
| 324 µF | 330 µF | 340 µF | 350 µF |
| 370 µF | 378 µF | 380 µF | 390 µF |
| 400 µF | 420 µF | 430 µF | 450 µF |
| 460 µF | 470 µF | 510 µF | 560 µF |
| 620 µF | 680 µF | 750 µF | 820 µF |
| 910 µF | 1000 µF | 1100 µF | 1200 µF |
| 1300 µF | 1500 µF | 1600 µF | 1800 µF |
| 2000 µF | 2200 µF | 2400 µF | 2700 µF |
| 3000 µF | 3300 µF | 3600 µF | 3900 µF |
| 4300 µF | 4700 µF | 5100 µF | 5600 µF |
| 6200 µF | 6800 µF | 7500 µF | 8200 µF |
| 9100 µF | |||
How Does The Capacitor Combination or Replacement Calculator Works
Introduction
Our calculator becomes vital when one wants to determine an appropriate set of capacitors that can be paralleled together to obtain a specific equivalent capacitance. Our Capacitor Replacement Calculator comes with a straightforward interface, making it easy for learners and hobbyists to do series and parallel calculations for capacitance in circuits.
What is Equivalent Capacitance?
When capacitors are connected in series, parallel, or in any other combination, they will combine to create an overall or equivalent capacitance. In ideal conditions, without the inclusion of other parameters, it works as a single capacitor.
Calculation Methods
The calculator operates by using an array of standard capacitor values, ranging from very small to large values. When you input the values of the equivalent capacitor, the calculator looks at all possible combinations of the standard values in the array to find the most accurate possible equivalent capacitance. Here's how it does it:
Series Combinations
How can I find total capacitance when I have a series combination? When capacitors are connected in series, it is obtained by adding reciprocal values of all individual capacitors according to this formula:
\(C_{\text{total}} = \frac{1}{\left(\frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}\right)}\)
to find the value of the equivalent capacitor.
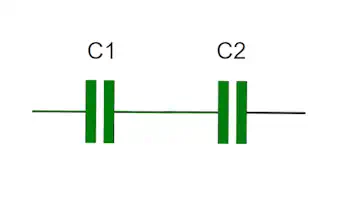
Parallel Combinations
How do I find the total capacitance of a circuit in parallel? All we need to do is sum up the individual capacitances. The calculator uses the formula:
\(C_{\text{total}} = C_1 + C_2 + \cdots + C_n\)
to find the value of the equivalent capacitance.
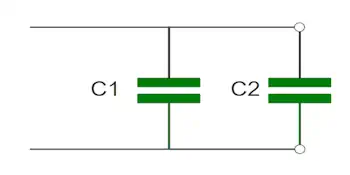
Mixed Combinations
For more complicated configurations, the calculator makes a combination of series and parallel connections. Firstly, it calculates the parallel capacitances and then considers the result as a single capacitor in a series combination, or vice versa, to achieve the targeted capacitance.
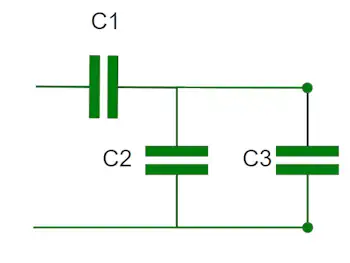
Example
For example, if you want to have a capacitor with a total capacitance of 10 µF, the calculator could suggest combining a 5 µF and another 5 µF capacitor in parallel or combining two 20 µF capacitors in series. It also can find a mixed configuration of a 4 µF + 4 µF in series with 8 µF in parallel.
What are the basic rules when replacing a capacitator?
What are the basic rules when replacing a capacitator?
While changing a capacitor, it should be ensured that some conditions are met for it to work well in circuitry. These fundamental rules are:
- Capacitance Value: The replacement capacitor should have a similar capacitance value to the original one or only differ within an acceptable tolerance limit.
- Physical Size and Lead Spacing: The available space and PCB layout should match the physical size and lead spacing of the replacement capacitor.
- Voltage Rating:The voltage rating of any substitute capacitor has to be either equal to or above that of the original capacitor's voltage rating.
- Type of Capacitor: The type (e.g., ceramic, electrolytic, film) should meet the requirements of the particular circuit.
Why Use Equivalent Capacitors in Series and Parallel Combination?
Series And Parallel Combinations Of Capacitors Can Have Following Benefits:
- Custom Capacitance Values: Get specific capacitance values that you have tailored to individual circuit requirements.
- Improved Performance: It is possible to increase component reliability, longevity by reducing ESR or increasing voltage rating in a series combination.
- Availability: Easier to find standard capacitor values that can be combined to meet the specific capacitance value.
Why Use Our Capacitor Combination or Replacement Calculator?
Our powerful calculator will help you save time and effort while working on your electronics projects. It will help you quickly build an equivalent capacitor from a list of standard or frequently used capacitance values. Whether you need to achieve a specific total capacitance through series, parallel, or mixed configurations, this calculator simplifies the process by providing precise combinations.
Benefits of Using Our Calculator
- Convenience: By offering series, parallel, and mixed configurations, the calculator gives you multiple options to achieve your desired capacitance. This is useful when restricted to a small number of capacitor values are available.
- Efficiency: Manually calculating all possible combinations of capacitors is time-consuming and leads to errors. This calculator automates this task, allowing you to concentrate more on creativity within your work.
- Accuracy: The calculator uses mathematical formulas so as to give accurate and reliable combinations. This can reduce the risk of calculation errors in your projects. professional engineer; its application is a good choice.
- Optimization: Most optimum combinations are obtained by considering factors such as acceptable error margins and practical constraints on the tool. This ensures that the suggested combinations are both accurate and efficient in real-world applications.
Frequently Asked Questions (FAQ)
What is a capacitor combination or replacement calculator?
A capacitor combination calculator is a tool used to find the most accurate set of capacitors necessary to achieve the total capacitance required. This means it uses series, parallel, and mixed configurations to give you correct combinations from standard capacitor values.
How does the capacitor combination calculator work?
For achieving an equivalent capacitance with maximum accuracy, this calculator examines all possible combos of standard capacitor values. In order for these results to be accurate, mathematical formulas are used to calculate series, parallel, and mixed combinations, ensuring precision and reliability.
Why should I use a capacitor replacement calculator?
By utilizing a capacitor combination calculator, finding the right combinations of capacitors becomes automated, thereby saving time and energy.
About the Author
Adilson Fernandes is a Experienced Electronic Engineer with with an Engineer's degree focused in Telecommunications Engineering. He is a web developer since 2014 and has been specialized making web-based calculators like Coolconversion.com and many others.

References
- University of Central Florida Pressbooks - Capacitors in Series and in Parallel – University Physics Volume 2
- SmartDraw - Circuit Diagram Maker | Free Online App.

