How Can One Make a 12 Ω Resistor Using a Combination of Other Resistors?
See below how to make a 12 Ω equivalent resistor by using other different resistors.
Resistor Replacement Calculator
Change the value in the box below. Then select the tolerance level and unit, and press "Calculate"
Answer
Below you can find a series of resistor combinations to replace a 12 Ω resistor.
Series Combinations:
For two resistors in series, the total resistance is calculated as:
\(R_{total} = R_1 + R_2\)
For example, with 3.9 Ω + 8.2 Ω in series = 12.1 Ω (error: 0.83%)
\(R_{total} = 3.9 Ω + 8.2 Ω \approx 12.1 Ω\)
- 3.9 Ω + 8.2 Ω in series = 12.1 Ω (error: 0.83%)
- 2.2 Ω + 10 Ω in series = 12.2 Ω (error: 1.67%)
- 5.6 Ω + 6.8 Ω in series = 12.4 Ω (error: 3.33%)
- 3.3 Ω + 8.2 Ω in series = 11.5 Ω (error: 4.17%)
- 4.7 Ω + 6.8 Ω in series = 11.5 Ω (error: 4.17%)
- 2.7 Ω + 10 Ω in series = 12.7 Ω (error: 5.83%)
- 5.6 Ω + 5.6 Ω in series = 11.2 Ω (error: 6.67%)
- 4.7 Ω + 8.2 Ω in series = 12.9 Ω (error: 7.5%)
- 2.7 Ω + 8.2 Ω in series = 10.9 Ω (error: 9.17%)
- 3.3 Ω + 10 Ω in series = 13.3 Ω (error: 10.83%)
- 3.9 Ω + 6.8 Ω in series = 10.7 Ω (error: 10.83%)
- 2.2 Ω + 8.2 Ω in series = 10.4 Ω (error: 13.33%)
- 6.8 Ω + 6.8 Ω in series = 13.6 Ω (error: 13.33%)
- 4.7 Ω + 5.6 Ω in series = 10.3 Ω (error: 14.17%)
Parallel Combinations:
For two resistors in parallel, the total resistance is calculated as:
\(R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}\)
For example, with 22 Ω + 27 Ω in parallel = 12.12 Ω (error: 1%)
\(R_{total} = \frac{1}{\frac{1}{22} + \frac{1}{27}} \approx 12.12 Ω\)
- 22 Ω + 27 Ω in parallel = 12.12 Ω (error: 1%)
- 15 Ω + 56 Ω in parallel = 11.83 Ω (error: 1.42%)
- 15 Ω + 68 Ω in parallel = 12.29 Ω (error: 2.42%)
- 18 Ω + 39 Ω in parallel = 12.32 Ω (error: 2.67%)
- 18 Ω + 33 Ω in parallel = 11.65 Ω (error: 2.92%)
- 15 Ω + 47 Ω in parallel = 11.37 Ω (error: 5.25%)
- 22 Ω + 22 Ω in parallel = 11 Ω (error: 8.33%)
- 18 Ω + 47 Ω in parallel = 13.02 Ω (error: 8.5%)
- 15 Ω + 39 Ω in parallel = 10.83 Ω (error: 9.75%)
- 18 Ω + 27 Ω in parallel = 10.8 Ω (error: 10%)
- 22 Ω + 33 Ω in parallel = 13.2 Ω (error: 10%)
- 27 Ω + 27 Ω in parallel = 13.5 Ω (error: 12.5%)
- 18 Ω + 56 Ω in parallel = 13.62 Ω (error: 13.5%)
- 15 Ω + 33 Ω in parallel = 10.31 Ω (error: 14.08%)
Mixed Combinations:
- 18 Ω + 18 Ω in series with 18 Ω in parallel = 12 Ω (exact)
- 27 Ω + 33 Ω in series with 15 Ω in parallel = 12 Ω (exact)
- 33 Ω + 27 Ω in series with 15 Ω in parallel = 12 Ω (exact)
- 6.8 Ω + 22 Ω in parallel with 6.8 Ω in series = 11.99 Ω (error: 0.08%)
- 22 Ω + 6.8 Ω in parallel with 6.8 Ω in series = 11.99 Ω (error: 0.08%)
- 5.6 Ω + 12 Ω in parallel with 8.2 Ω in series = 12.02 Ω (error: 0.17%)
- 6.8 Ω + 12 Ω in series with 33 Ω in parallel = 11.98 Ω (error: 0.17%)
- 12 Ω + 5.6 Ω in parallel with 8.2 Ω in series = 12.02 Ω (error: 0.17%)
- 12 Ω + 6.8 Ω in series with 33 Ω in parallel = 11.98 Ω (error: 0.17%)
- 2.7 Ω + 8.2 Ω in parallel with 10 Ω in series = 12.03 Ω (error: 0.25%)
- 8.2 Ω + 2.7 Ω in parallel with 10 Ω in series = 12.03 Ω (error: 0.25%)
- 10 Ω + 18 Ω in parallel with 5.6 Ω in series = 12.03 Ω (error: 0.25%)
- 18 Ω + 10 Ω in parallel with 5.6 Ω in series = 12.03 Ω (error: 0.25%)
- 8.2 Ω + 18 Ω in series with 22 Ω in parallel = 11.96 Ω (error: 0.33%)
- 12 Ω + 47 Ω in series with 15 Ω in parallel = 11.96 Ω (error: 0.33%)
- 18 Ω + 8.2 Ω in series with 22 Ω in parallel = 11.96 Ω (error: 0.33%)
- 22 Ω + 39 Ω in series with 15 Ω in parallel = 12.04 Ω (error: 0.33%)
- 39 Ω + 22 Ω in series with 15 Ω in parallel = 12.04 Ω (error: 0.33%)
- 47 Ω + 12 Ω in series with 15 Ω in parallel = 11.96 Ω (error: 0.33%)
- 6.8 Ω + 15 Ω in series with 27 Ω in parallel = 12.06 Ω (error: 0.5%)
- 15 Ω + 6.8 Ω in series with 27 Ω in parallel = 12.06 Ω (error: 0.5%)
- 4.7 Ω + 18 Ω in parallel with 8.2 Ω in series = 11.93 Ω (error: 0.58%)
- 18 Ω + 4.7 Ω in parallel with 8.2 Ω in series = 11.93 Ω (error: 0.58%)
- 3.3 Ω + 5.6 Ω in parallel with 10 Ω in series = 12.08 Ω (error: 0.67%)
- 5.6 Ω + 3.3 Ω in parallel with 10 Ω in series = 12.08 Ω (error: 0.67%)
- 6.8 Ω + 8.2 Ω in parallel with 8.2 Ω in series = 11.92 Ω (error: 0.67%)
- 8.2 Ω + 6.8 Ω in parallel with 8.2 Ω in series = 11.92 Ω (error: 0.67%)
- 15 Ω + 18 Ω in parallel with 3.9 Ω in series = 12.08 Ω (error: 0.67%)
- 15 Ω + 47 Ω in series with 15 Ω in parallel = 12.08 Ω (error: 0.67%)
- 18 Ω + 15 Ω in parallel with 3.9 Ω in series = 12.08 Ω (error: 0.67%)
- 47 Ω + 15 Ω in series with 15 Ω in parallel = 12.08 Ω (error: 0.67%)
- 8.2 Ω + 27 Ω in series with 18 Ω in parallel = 11.91 Ω (error: 0.75%)
- 27 Ω + 8.2 Ω in series with 18 Ω in parallel = 11.91 Ω (error: 0.75%)
- 8.2 Ω + 15 Ω in parallel with 6.8 Ω in series = 12.1 Ω (error: 0.83%)
- 12 Ω + 18 Ω in parallel with 4.7 Ω in series = 11.9 Ω (error: 0.83%)
- 15 Ω + 8.2 Ω in parallel with 6.8 Ω in series = 12.1 Ω (error: 0.83%)
- 18 Ω + 12 Ω in parallel with 4.7 Ω in series = 11.9 Ω (error: 0.83%)
- 8.2 Ω + 27 Ω in parallel with 5.6 Ω in series = 11.89 Ω (error: 0.92%)
- 10 Ω + 27 Ω in series with 18 Ω in parallel = 12.11 Ω (error: 0.92%)
- 15 Ω + 22 Ω in series with 18 Ω in parallel = 12.11 Ω (error: 0.92%)
- 22 Ω + 15 Ω in series with 18 Ω in parallel = 12.11 Ω (error: 0.92%)
- 27 Ω + 8.2 Ω in parallel with 5.6 Ω in series = 11.89 Ω (error: 0.92%)
- 27 Ω + 10 Ω in series with 18 Ω in parallel = 12.11 Ω (error: 0.92%)
- 10 Ω + 12 Ω in series with 27 Ω in parallel = 12.12 Ω (error: 1%)
- 12 Ω + 10 Ω in series with 27 Ω in parallel = 12.12 Ω (error: 1%)
- 12 Ω + 15 Ω in series with 22 Ω in parallel = 12.12 Ω (error: 1%)
- 15 Ω + 12 Ω in series with 22 Ω in parallel = 12.12 Ω (error: 1%)
- 18 Ω + 39 Ω in series with 15 Ω in parallel = 11.88 Ω (error: 1%)
- 39 Ω + 18 Ω in series with 15 Ω in parallel = 11.88 Ω (error: 1%)
How to Use This Calculator
To use this Resistor Replacement Calculator, enter the desired equivalent resistance value into the field provided, select a tolerance level, and then click on 'Calculate.' The calculator will find hundreds of combinations and choose the best ones. You will be presented with various combinations consisting of resistors with respective percentage errors or exact values, enabling you to decide on which option is most suitable.
How Does The Resistor Replacement Calculator Work
Introduction
Our calculator assists in deciding which set of resistors can be put together to achieve specific equivalent resistance. If you need a resistor you don't have in your kit, you can make another resistor with the same resistance by using other resistors that you have. This calculator is like a reverse series and parallel calculatior for resistance in circuits.
What is Equivalent Resistance?
When resistors are connected in series, parallel, or any other combination, they combine to produce an overall or equivalent resistance. In ideal conditions, it acts as one resistor.
Calculation Methods
The calculator uses arrays of standard resistor values spanning from very small to large values. When you put the values of the equivalent resistor into it, it screens all possible combinations among these standard values so as to pick out the one that gives the closest approximation to the actual equivalent resistance possible. Here's how:
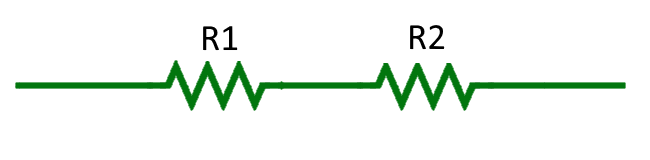
Series Combinations
Resistors connected in series have their total resistance obtained by adding up individual resistors' values such that
\(R_{\text{total}} = R_1 + R_2 + \cdots + R_n\)
to determine the equivalent resistor's value.
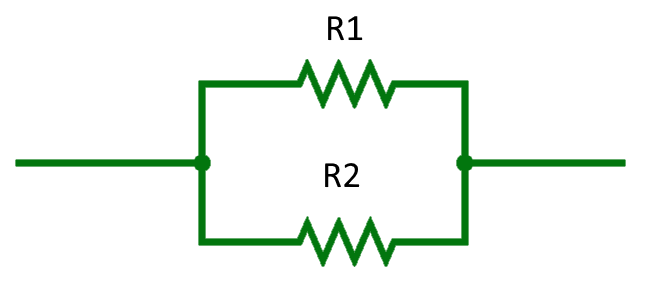
Parallel Combinations
When resistors are connected in parallel, the total resistance is found by summing the reciprocals of the individual resistances. The calculator uses the formula:
\(R_{\text{total}} = \frac{1}{\left(\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}\right)}\)
to figure out the value of the equivalent resistance.
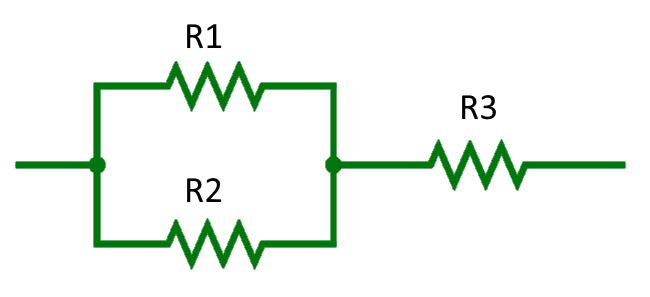
Mixed Combinations
Similarly, the calculator can also make a combination of series and parallel connections. First, it evaluates parallel resistances (R1 ∥ R2) and then takes this output as a single resistor in series with the third resistor (R3), or vice versa, to achieve the desired resistance.
Example
Supose you want a resistor having a total resistance equal to 100 Ohms, then the calculator may recommend to combine two 200 Ohms in parallel or two 50 Ohms in series. It has an option for even a mixed configuration like 60 Ohms + 60 Ohms in series and 120 Ohms in parallel.
The basic rules when replacing a resistor?
What are the basic rules when replacing a resistor?
When replacing a resistor, it must be ensured that some conditions are met for it to work as expected. These requirements are:
- Resistance Value: The replacement resistor should have about the same value of resistance as that of the original component or vary only up to some acceptable tolerance limit. Remenber that there are different tolerances (1, 5, 10, or 20 %). Try to use 1% if possible.
- Power Rating: To keep the power dissipation from overheating, a replacement resistor must have an equal or higher power rating. If you don't know how to calculate the power dissipated in these configurantion of resitors, read Range of Power for Parallel Resistors, Range of Power for Series Resistors and Range of Power for Series-Parallel Resistors.
- Type of Resistor: The type (for example, carbon film, metal film, wire-wound) should be in line with certain requirements of that circuit.
Benefits of Using Our Calculator
- Convenience: Offering multiple options like series, parallel, and mixed configurations allows users to get their desired resistance using varied techniques. This is helpful when a small quantity of resistor values are in hand.
- Efficiency: Manually performing calculations for each possible combination is both time-consuming and prone to errors. Therefore, this tool was designed to ease your work by automating it, hence allowing more time for creativity in your work.
- Accuracy: Combinations provided by the calculator are precise since they are derived from mathematical equations and a tested algorthm. Consequently, the possibility of calculation errors decreases within your project's scope.
- Optimization: THe calculator ensures that suggested combinations remain accurate while being efficient as well as taking into account acceptable error margins, hence providing optimum combinations among hundreds or thousands posiible.
Resistor Values Tables for the Main Series in Ohms
Our Resistor Replacement Calculator works by combining the values of resistances in parallel, series, or mixed configurations. It uses the following standard resistance values to find the best equivalent resistor configurations. Each value is measured in ohms (Ω).
About the Author
Adilson Fernandes is a Experienced Electronic Engineer with with an Engineer's degree focused in Telecommunications Engineering. He is a web developer since 2014 and has been specialized making web-based calculators like Coolconversion.com and many others.
References
- Electronics-Notes.com - Standard Resistor Values: E3 E6 E12 E24 E48 E96 » Electronics Notes
- North Coast Synthesis Ltd. - Resistor Gallery
- British Columbia/Yukon Open Authoring Platform - 21.1 Resistors in Series and Parallel – College Physics: OpenStax